エムスリーテックブログ

エムスリー(m3)のエンジニア・開発メンバーによる技術ブログです

Go1.19に採用されたPattern-defeating Quicksortの紹介

Go

エムスリーエンジニアリンググループ AI・機械学習チームでソフトウェアエンジニアをしている中村(po3rin) です。検索とGoが好きです。

最近、Go1.19でsortパッケージのアルゴリズムが一部変更されました。

Pattern-defeating Quicksortが入った時のdiff

1.19リリースノートではPattern-defeating Quicksortが採用されたと紹介があります。実際にsort/zsortfunc.go、sort/zsortinterface.goにそれぞれpdqsort_func、pdqsortという関数があります。

// pdqsort sorts data[a:b].
// The algorithm based on pattern-defeating quicksort(pdqsort), but without the optimizations from BlockQuicksort.
// pdqsort paper: https://arxiv.org/pdf/2106.05123.pdf
// C++ implementation: https://github.com/orlp/pdqsort
// Rust implementation: https://docs.rs/pdqsort/latest/pdqsort/
// limit is the number of allowed bad (very unbalanced) pivots before falling back to heapsort.
func pdqsort(data Interface, a, b, limit int)

今回はPattern-defeating Quicksortがどのようなアルゴリズムなのかを論文*1を読んで、実際にGoでどのように使われているかを調べてみました。

この記事ではPattern-defeating Quicksortのざっくりとした理解を目的とし、証明など細かい話はスキップしてなんとなく何をやってるのかの理解を目指します。

Pattern-defeating Quicksortはクイックソートが苦手な同じ値を持つシーケンスに対して効力を発揮します。実用では大量の被りがある値のソートがほとんど(カテゴリでソートするとか)なので、実用面でも非常に有用なアルゴリズムです。

この論文の貢献として、k個の異なる要素を持つ入力に対してO(nk)の最悪ケースに収まる3 方向比較手法を提案しており非常に面白いです。

論文はこちらです。

arxiv.org

Pattern-defeating Quicksort 概要

Pattern-defeating Quicksort は近年利用されるハイブリッドソートアルゴリズムであるイントロソート*2を拡張および改良したものです。クイックソートと最悪時にフォールバックするヒープソートを組み合わせます。

後で詳しく説明していきますが、Pattern-defeating Quicksortの肝は簡単に言うと

  • パーティション処理をいい感じにした
  • 最悪ケースを検知してフォールバックするようにした

の2つです。

イントロソートの簡単な復習

Pattern-defeating Quicksortはイントロソートの改良版なので、簡単にイントロソートを復習しておきます。

イントロソートは近年最も使用されているハイブリッドソートアルゴリズムで、挿入ソート、ヒープソート、クイックソートを組み合わせたハイブリッドアルゴリズムです。ヒューリスティックな方法で、いつどの戦略を採用するかを決定します。基本はクイックソートで、例えば、再帰の深さが深くなりすぎるとヒープソートに切り替えたり、パーティションのサイズが小さくなりすぎると挿入ソートに切り替えたりします。

オランダ国旗問題の復習

Pattern-defeating Quicksortは3-way quicksortの考えがベースとなっており、3-way quicksortはオランダ国旗問題の考え方がベースになっているので、まずはオランダ国旗問題を復習します。

オランダ国旗問題は0、1、2のみを含む配列を同じ要素でパーティションする問題です。例えば下記のinをoutに変換する問題です。

オランダ国旗問題の例

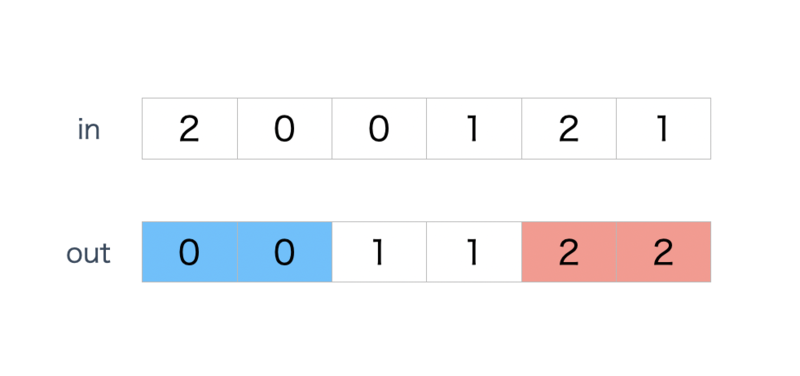
素朴なクイックソートの実装では、同じパーティションに同じ要素を配置することにより Θ( n^{2})の最悪ケースを引き起こす可能性があります。等しい要素を効率的に処理するには、ダイクストラのオランダ国旗問題に相当する3分割手法の考え方が必要です。

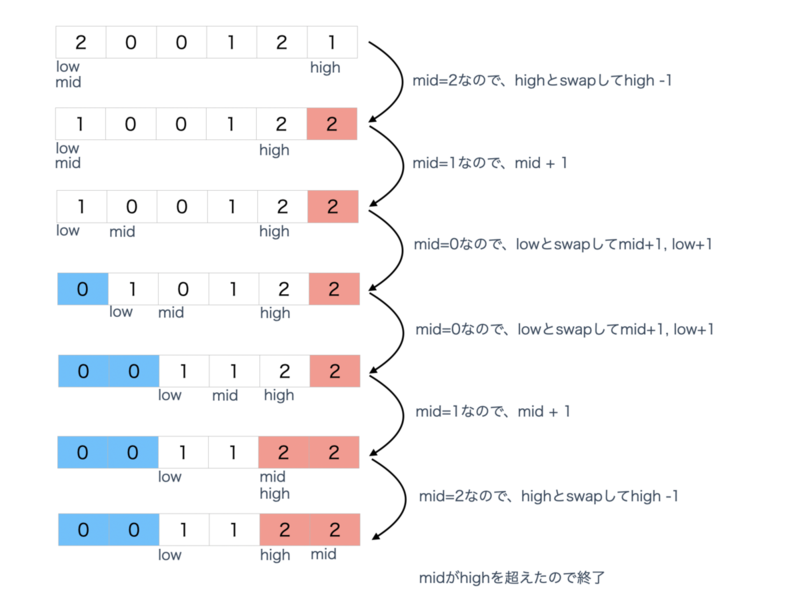
アルゴリズムは単純で線形時間で解けます。midとlowを配列の最初の要素にセットし、highを最後の要素にセットします。

もしmid=0なら: lowとmidの要素をswapしてhighでデクリメント
もしmid=1なら: midをインクリメント
もしmid=2なら: highとmidの要素をswapしてhighをデクリメント

実際にこのアルゴリズムを適用すると下記のようになります。

オランダ国旗問題を解く例

Goでオランダ国旗問題を解く関数はこうなります。

func sort(arr []int) []int {
    low := -1
    high := len(arr)

    for i := 0; i < high; {
        val := arr[i]
        switch val {
        case 0:
            arr[i], arr[low+1] = arr[low+1], arr[i]
            low++
            i++
        case 1:
            i++
        case 2:
            arr[i], arr[high-1] = arr[high-1], arr[i]
            high--
        }
    }
    return arr
}

Pattern-defeating Quicksort のパーティション

単純なクイックソートの実装では、等しい比較要素を同じパーティションに配置することにより Θ( n^{2})の最悪のケースが引き起こされる可能性があります。

等しい要素を効率的に処理するには、オランダ国旗問題と同等の三分割が必要になります。等しい要素を集めて、それより大きい要素、小さい要素の3分割ができれば、その後のソートで等しい要素を含むパーティションのソートをスキップできます。これが3-way quicksortの考え方です。

これはオランダ国旗問題と同じ単純な3分割問題として考えることができます。この論文では3-way quicksortのパーティションの取り方を改善し、 O(nlogn)のアルゴリズムの実用的な改善に取り組んでいます。

上記で説明したオランダの国旗問題の解法を単純に適用すると、要素がピボット(パーティションを組むために各要素と比較するための要素)より大きいか小さいに加え、**ピボットと等しいかどうかを毎回明示的にチェックする必要があるのでパフォーマンスが低下します。

この論文ではこの問題に対処する新しい手法を議論しており、k個の異なる要素を持つ入力に対して O(nk)の最悪ケースに収まる手法を提案しています。Pattern-defeating Quicksortではこの手法をベースにイントロソートを改良しています。

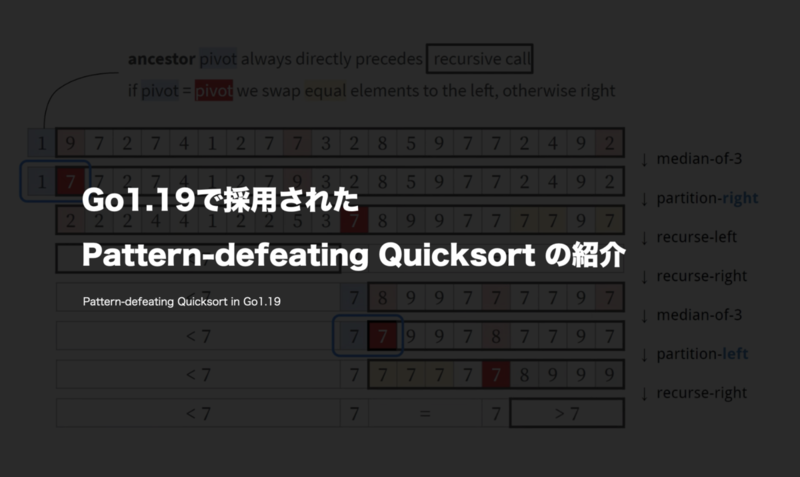
Pattern-defeating Quicksortは2つのパーティション関数を使用します。1つはピボットp以下の要素を左のパーティションにグループ化(partition left)し、もう1つはピボット以上要素を右のパーティション(partition right)にグループ化します。下図論文から引用した図で、partition right関数の処理を追ったものです。

partition_rightの処理

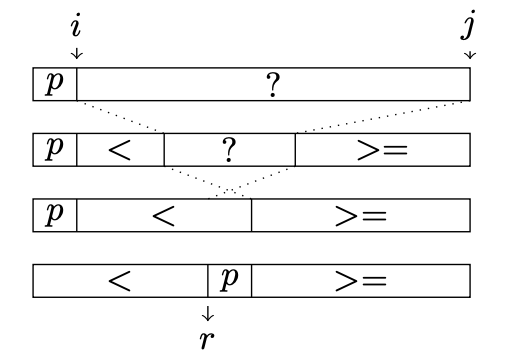
最初のステップ図は初期状態であり、 pはパーティションの為のピボットであり、こちらはサブシーケンスの長さによって様々なピボット選択手法を使って選択します(後述)。swapのためにサブシーケンスの最初と最後のインデックスをそれぞれ i, jとし iをインクリメント、 jをデクリメントしていきながら要素をswapしていき、ピボットが交差するとパーティション処理が終了し、最後にピボットを中央に配置します。最終的にピボットより小さい / ピボットと同じ値 / ピボット以上の3つに分けることができます。このパーティションの組み方の利点は「要素がピボットの値以上かどうか」という条件一個で判定できることです。

この二つの関数を利用して再帰的に配列をパーティションしていきます。例えば下記図のように、ピボット pで αをパーティションし、再帰的に右側のパーティションをピボット qとして βをパーティションしていきます。

再帰的にpartition関数を適用する

p が q に等しくない場合は、上記のステップを再帰的に適用します。最終的に p=qとなった時は、同じ値を真ん中に集めた3構成にできています。

partitionの処理の最終系

ちなみに、ある点 q で β が空になった場合、p に等しい要素はなく、α を最初に分割したときに 3 分割が行われたと結論付けることができます。

こちらを利用することで k個の異なる要素を持つ入力に対して分割が O(nk)の最悪ケースに収まります。これによってクイックソートの苦手な同じ値を持つ要素を集めて処理ができます。

具体的なシーケンスで見ていきます。例は論文を書いたOrsonによるCWI Database Architecturesでの発表から引用します。

Orsonによる発表スライドから引用

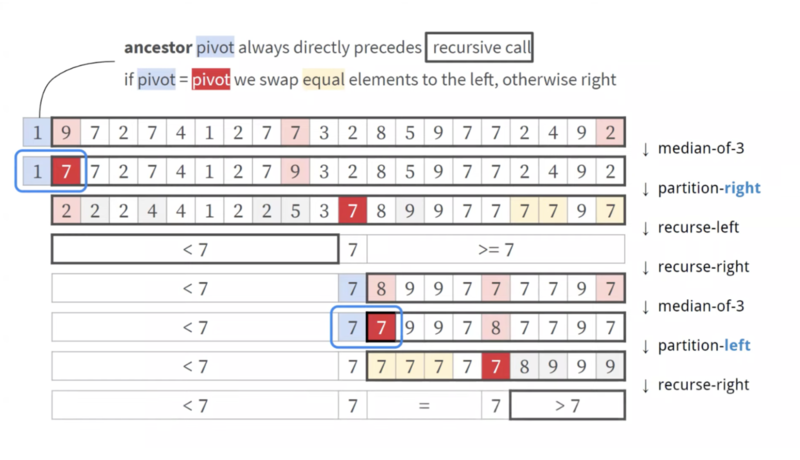
この例ではピボットをシンプルに最初、中央、最後の3つの値の中央値として採用しています(入力が大きい時は後述の手法でピボットを決める)。最終的に「7より小さい、7に等しい、7より大きい」の3つに分割できていることがわかります。

ピボット選択の方法~John Tukey’s ninther~

ピボットの選択において、不均衡パーティションを避けるためにシーケンスの中央値を選択することが理想です。厳密な中央値を計算するにはすべてのデータポイントを保存し、それらを並べ替えて中間値を選択する必要があるので大きな入力の場合はパフォーマンスの問題が発生します

そこで論文ではJohn Tukey’s ninther*3という手法でピボットを選択します。シーケンスを3つに分けてそれぞれ中央値を計算し、3つの中央値の中央値を取ります。

3, 1, 4, 4, 5, 9, 9, 8, 2

a = median( 3, 1, 4 ) = 3
b = median( 4, 5, 9 ) = 5
c = median( 9, 8, 2 ) = 8

m = median(a, b, c) = 5

この方法であれば素早く大雑把な中央値の近似が得られます。

実際のGoの実装ではピボットを選択するサブシーケンスの長さによってピボット選択方法を切り替えます。長さが8以下なら単純に中央値をとり、50以下なら単純にサブシーケンスの最初と中央と最後の3つの値の中央値をとり、50以上ならJohn Tukey’s nintherを利用します。

// choosePivot chooses a pivot in data[a:b].
//
// [0,8): chooses a static pivot.
// [8,shortestNinther): uses the simple median-of-three method.
// [shortestNinther,∞): uses the Tukey ninther method.
func choosePivot(data Interface, a, b int) (pivot int, hint sortedHint)

Pattern-defeating Quicksort の不良パーティション対処

Pattern-defeating Quicksortは、指定したピボットパーセンタイルtex: pよりも不均衡なパーティションを不良パーティションと呼びます(ちなみにピボットパーセンタイル p=1/2だと理想的はパーティションになります)。

例えば下記のようなシーケンスでピボットパーセンタイル1/10のポイント(今回は1)を採用してしまうとほとんどパーティションが機能しません。

[2, 2, 5, 4, 7, 1, 3, 6, 9, 3]

↓ pivot=1

[1 / 2, 2, 5, 4, 7, 3, 6, 9, 3]

Yuval Filmus*4 は p = 1/2 の最適なケースと比較してクイックソートの速度低下を調べました(下図)。

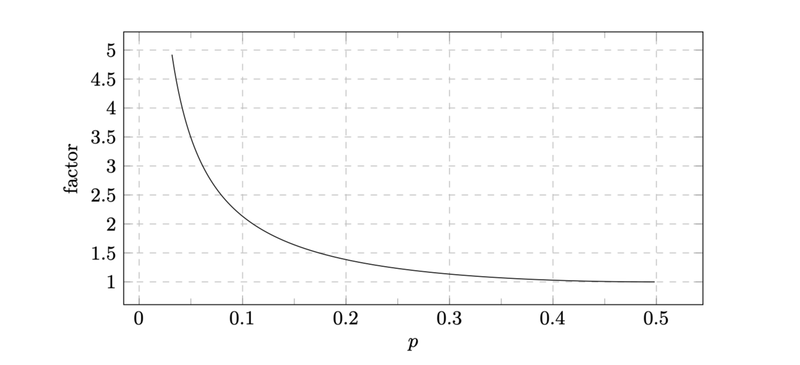
Yuval Filmusによるクイックソートのピボットパーセンタイルとパフォーマンスの影響

このグラフから、例えば p=0.25の場合は、理想的な場合と比べて40%だけ遅くなることがわかります。

p=0.1を下回るとパフォーマンスの低下が激しくなることもわかります。このため、 pの閾値を設定し、それより下回る不良パーティションのケースが多ければフォールバックする戦略を取ります。

シーケンスの長さを nとすると、不良パーティションを複数回遭遇するのを回避するために下記ステップを行います。

  • カウンターを \log_{2} nの整数部に設定します
  • 不良パーティションに遭遇するたびに、カウンターをデクリメントします
  • 再帰呼び出しの開始時にカウンターが 0の場合、クイックソートではなく、ヒープソートを使用

論文ではこのピボットパーセンタイル pの閾値を 0.125としておりGoも 0.125になっています。このスキームの利点は、アーキテクチャが変更された場合(ヒープソートの代わりに別の最悪のケースのソートアルゴリズムを使用している場合など)に、それに合わせて pを調整できることです(Goの場合は 0.125がハードコードされていて変更はできない)。

Goではpdqsort関数のlimit引数がカウンターにあたり、これが0になるとヒープソートに切り替わります。

// pdqsort sorts data[a:b].
// The algorithm based on pattern-defeating quicksort(pdqsort), but without the optimizations from BlockQuicksort.
// pdqsort paper: https://arxiv.org/pdf/2106.05123.pdf
// C++ implementation: https://github.com/orlp/pdqsort
// Rust implementation: https://docs.rs/pdqsort/latest/pdqsort/
// limit is the number of allowed bad (very unbalanced) pivots before falling back to heapsort.
func pdqsort(data Interface, a, b, limit int) {
    // ...

    for {
        // ...

        // Fall back to heapsort if too many bad choices were made.
        if limit == 0 {
            heapSort(data, a, b)
            return
        }

    // ...
}

ちなみにちょっとした工夫として、カウンターを配列の長さの所要ビット数として \log_{2} nを計算しています。

// Sort sorts data in ascending order as determined by the Less method.
// It makes one call to data.Len to determine n and O(n*log(n)) calls to
// data.Less and data.Swap. The sort is not guaranteed to be stable.
func Sort(data Interface) {
    n := data.Len()
    if n <= 1 {
        return
    }
    limit := bits.Len(uint(n))
    pdqsort(data, 0, n, limit)
}

Go の Pattern-defeating Quicksort

Goに実装されたPattern-defeating Quicksortは論文と比べて下記のような変更が加えられています。

  • BlockQuicksortを使った最適化を無効(今回は解説しませんでしたが将来追加される可能性はありそう)
  • ベンチマーク結果に従って、いくつかのパラメーターを変更

Goにおけるベンチマークはissue:50154で提出されています。

EC2 t2.micro (1 vCPU, 1 GiB mem), goos: linux, goarch: amd64

name                       old time/op    new time/op    delta
Random/sort_64               6.57µs ± 2%    6.67µs ± 1%   +1.52%  (p=0.002 n=10+9)
Random/sort_256              30.6µs ± 5%    31.2µs ± 5%     ~     (p=0.052 n=10+10)
Random/sort_1024              142µs ± 1%     144µs ± 1%   +1.73%  (p=0.000 n=10+10)
Random/sort_4096              674µs ± 1%     674µs ± 0%     ~     (p=0.739 n=10+10)
Random/sort_65536            14.2ms ± 0%    14.1ms ± 0%   -0.68%  (p=0.000 n=10+10)
Sorted/sort_64               2.87µs ± 4%    1.31µs ± 8%  -54.49%  (p=0.000 n=10+10)
Sorted/sort_256              11.7µs ± 0%     2.4µs ± 3%  -79.34%  (p=0.000 n=10+10)
Sorted/sort_1024             54.8µs ± 6%     7.0µs ± 2%  -87.31%  (p=0.000 n=10+10)
Sorted/sort_4096              253µs ± 1%      25µs ± 1%  -90.31%  (p=0.000 n=9+10)
Sorted/sort_65536            5.53ms ± 0%    0.35ms ± 1%  -93.61%  (p=0.000 n=9+10)
NearlySorted/sort_64         3.36µs ± 1%    3.13µs ± 5%   -6.69%  (p=0.000 n=8+10)
NearlySorted/sort_256        14.7µs ± 1%    13.2µs ± 1%   -9.63%  (p=0.000 n=9+8)
NearlySorted/sort_1024       69.2µs ± 4%    59.6µs ± 1%  -13.94%  (p=0.000 n=10+8)
NearlySorted/sort_4096        320µs ± 1%     283µs ± 1%  -11.45%  (p=0.000 n=9+10)
NearlySorted/sort_65536      6.79ms ± 0%    6.03ms ± 1%  -11.17%  (p=0.000 n=9+10)
Reversed/sort_64             3.25µs ± 3%    1.53µs ± 8%  -52.90%  (p=0.000 n=8+10)
Reversed/sort_256            12.7µs ± 2%     3.1µs ± 3%  -75.43%  (p=0.000 n=10+10)
Reversed/sort_1024           55.5µs ± 1%     9.8µs ± 3%  -82.40%  (p=0.000 n=9+10)
Reversed/sort_4096            265µs ± 1%      36µs ± 3%  -86.58%  (p=0.000 n=10+8)
Reversed/sort_65536          5.68ms ± 0%    0.51ms ± 0%  -90.98%  (p=0.000 n=9+10)
NearlyReversed/sort_64       4.44µs ± 1%    3.93µs ± 2%  -11.38%  (p=0.000 n=7+9)
NearlyReversed/sort_256      21.1µs ± 1%    16.8µs ± 1%  -20.16%  (p=0.000 n=10+10)
NearlyReversed/sort_1024     96.8µs ± 3%    77.3µs ± 2%  -20.13%  (p=0.000 n=10+9)
NearlyReversed/sort_4096      453µs ± 1%     365µs ± 1%  -19.42%  (p=0.000 n=10+10)
NearlyReversed/sort_65536    9.22ms ± 0%    7.40ms ± 2%  -19.75%  (p=0.000 n=8+10)
Mod8/sort_64                 3.39µs ± 4%    3.32µs ± 7%     ~     (p=0.190 n=9+10)
Mod8/sort_256                12.5µs ± 1%    10.3µs ± 1%  -17.87%  (p=0.000 n=10+10)
Mod8/sort_1024               49.1µs ± 6%    39.6µs ± 6%  -19.43%  (p=0.000 n=9+10)
Mod8/sort_4096                200µs ± 2%     149µs ± 2%  -25.53%  (p=0.000 n=10+10)
Mod8/sort_65536              2.98ms ± 0%    2.20ms ± 1%  -26.34%  (p=0.000 n=10+10)
AllEqual/sort_64             1.68µs ± 6%    1.33µs ± 7%  -20.73%  (p=0.000 n=10+10)
AllEqual/sort_256            3.94µs ± 1%    2.49µs ± 3%  -36.69%  (p=0.000 n=9+10)
AllEqual/sort_1024           12.9µs ± 1%     6.9µs ± 3%  -46.14%  (p=0.000 n=9+10)
AllEqual/sort_4096           46.4µs ± 5%    24.8µs ± 1%  -46.68%  (p=0.000 n=10+8)
AllEqual/sort_65536           697µs ± 0%     352µs ± 1%  -49.50%  (p=0.000 n=10+10)
[Geo mean]                   78.7µs         40.8µs       -48.17%

ランダムケースでは若干パフォーマンスが落ちているケースもありますが、ほとんどの場合でパフォーマンスが大幅に改善しています。

まとめ

今回はGo1.19で採用されたPattern-defeating Quicksortの概要を紹介し、パーティション処理やピボット選択、不良パーティション検知で、クイックソートの最悪ケースを回避できるように工夫されていることを学びました。

Go1.19にアップグレードしてsortパッケージがどれくらい速くなったか是非試してみてください。より細かい工夫や、詳しい証明などは論文を参照ください。

We are Hiring!

エムスリーではGoで医療に貢献していきたいメンバーを募集しています。エムスリーではGoが至る所で採用されています。

  • 各種API(アプリケーション、検索、レコメンド、リランキング等)
  • レコメンドAPI
  • データ連携Batch
  • Push通知基盤
  • 各種便利ツールの開発

ソフトウェアエンジニアだけでなく、MLエンジニアもGoが書けるという異質な環境なので、Goを書いてみたい人には面白い環境かもしれません。 「ちょっと話を聞いてみたいかも」という人はこちらから！

jobs.m3.com

参照

*1:arxiv.org

*2:https://dl.acm.org/doi/10.5555/261387.261395

*3:https://www.sciencedirect.com/science/article/pii/B9780122047503500241?via%3Dihub

*4:https://cs.stackexchange.com/questions/31928/solving-recurrence-relation-with-two-recursive-calls/31930#31930